

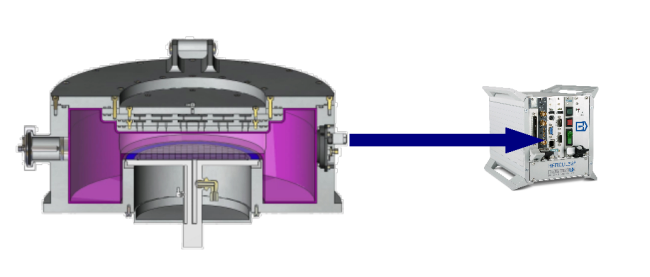
| Hercules®
in connection with the process
chamber |
|---|
 |
|
The Hercules®
Plasma Metrology System is based on the Self
Excited Electron
Plasma Resonance Spectroscopy
(SEERS) for
low pressure and on Nonlinear
Extended
Electron
Dynamics
(NEED) for
medium pressure. |
| RF discharge: |
 The capacitive
driven radio frequency (RF) discharge is
commonly used for materials processing. However, the required
processing (etching, deposition) of such discharges is generally the
result of poorly understood physical and
chemical processes occurring
in the gas phase and at the gas/solid interface. In this respect, the
role of the sheaths in front of the electrodes is of fundamental
importance for the understanding of the discharge physics of the
asymmetrical capacitively coupled RF discharge. Due to their
small mass
(large mobility) and high temperature, the electrons strive to leave
the bulk plasma. The sheath (dark space) keeps the
electrons within the bulk plasma (shielding) by a retarding electric
field build-up when electrons leave the outer regions
of the plasma. The electrons-neutrals collisions take place in
the bulk plasma where ions and electrons are created. The
radicals for etching are formed in the bulk plasma. The ions move to
the sheaths. The acceleration of ions provides
energy for etching. This energy can be increased by external (RF)
potentials. The capacitive
driven radio frequency (RF) discharge is
commonly used for materials processing. However, the required
processing (etching, deposition) of such discharges is generally the
result of poorly understood physical and
chemical processes occurring
in the gas phase and at the gas/solid interface. In this respect, the
role of the sheaths in front of the electrodes is of fundamental
importance for the understanding of the discharge physics of the
asymmetrical capacitively coupled RF discharge. Due to their
small mass
(large mobility) and high temperature, the electrons strive to leave
the bulk plasma. The sheath (dark space) keeps the
electrons within the bulk plasma (shielding) by a retarding electric
field build-up when electrons leave the outer regions
of the plasma. The electrons-neutrals collisions take place in
the bulk plasma where ions and electrons are created. The
radicals for etching are formed in the bulk plasma. The ions move to
the sheaths. The acceleration of ions provides
energy for etching. This energy can be increased by external (RF)
potentials. |
| Understanding the real world - SEERS theory: |
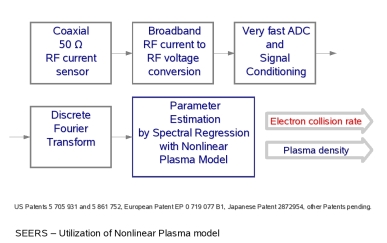 Nonlinear effects
like the I-V-characteristic of the
boundary sheath are utilized for Langmuir probe measurements but they
are usually neglected for modeling of RF discharges due to their very
inconvenient mathematical treatment. The Self Excited Electron Plasma
Resonance Spectroscopy (SEERS) utilizes exactly these nonlinear effects
and known resonance effects in RF discharges [1].
The nonlinear elements, in particular the sheathes, provide harmonics
in the discharge current and excite the plasma and the sheath at their
series resonance characterized by the so-called geometric resonance
frequency [2]. Nonlinear effects
like the I-V-characteristic of the
boundary sheath are utilized for Langmuir probe measurements but they
are usually neglected for modeling of RF discharges due to their very
inconvenient mathematical treatment. The Self Excited Electron Plasma
Resonance Spectroscopy (SEERS) utilizes exactly these nonlinear effects
and known resonance effects in RF discharges [1].
The nonlinear elements, in particular the sheathes, provide harmonics
in the discharge current and excite the plasma and the sheath at their
series resonance characterized by the so-called geometric resonance
frequency [2]. |
| The bulk model: |
The model of the plasma bulk is
based on a 2d-fluid model with zero order moment of the
Boltzmann
equation and the first order moment 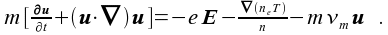 A uniform plasma yields 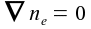 with the above moments of the Boltzmann equation the permittivity of the plasma 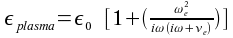 . The full set of the Maxwellian equations leads now to the Helmholtz equation for the magnetic field H = F(r, z)
In a cylinder
geometry it can be satisfied by a fundamental system with a series in
Bessel functions
based here on the
azimuthal component of the magnetic
field
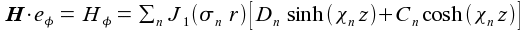 if, as already assumed above, the plasma density and so the the permittivity can be is assumed to be approximately constant. The coefficients are given though proper boundary conditions depending on the geometry. The total RF current is then given by 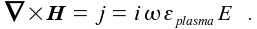 |
| The sheath model: |
The first three moments of the Boltzmann equation and the
Poisson equation describe the electron dynamics. Together with
a parameter ansatz for the ion distribution, boundary
conditions provide by a nonlinear
sheath
model (here simplified without pressure heating, see [4])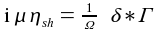 with the time varying, normalized sheath thickness δ. The convolution is denoted *, the normalization to fundamental plasma physical parameters is as follows 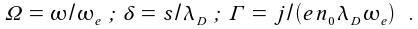 |
| The complete model and SEERS: |
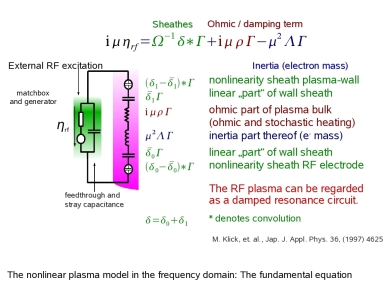 The
final model
depends
mainly on the averaged density of the electrons and
their collision rate. In the simple case of a one-dimensional
plasma, the fundamental equation can be reflected by equivalent circuit
as shown in the scheme. The fundamental equation is now a nonlinear
differential equation in the time domain or convolution equation in the
frequency domain. The
final model
depends
mainly on the averaged density of the electrons and
their collision rate. In the simple case of a one-dimensional
plasma, the fundamental equation can be reflected by equivalent circuit
as shown in the scheme. The fundamental equation is now a nonlinear
differential equation in the time domain or convolution equation in the
frequency domain.So three parameters must be estimated by minimizing an appropriate (mathematical) norm. This model-based determination of plasma parameters is called Self Excited Electron Resonance Spectroscopy (SEERS) [3-9]. SEERS provides the spatially and harmonically averaged electron plasma density and the effective electron collision rate. The electron collision rate comprises stochastic (pressure) heating and ohmic heating of the electrons. It depends via ohmic heating on the density of gas and so on the gas temperature [10-12]. 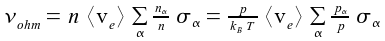 where νohm
is the electron collision rate
for
ohmic heating, n the density of neutrals,
nα
the density of species
α,
<ve> the mean electron
velocity, σα
the
(elastic)
cross section with
respect to species
α, p the pressure, kB
the Boltzmann constant, and T
the temperature. Thus in particular the electron
collision rate is an very important
indicator for the plasma process stability due to their dependence on
the process chemistry.
But it reflects also plasma process drift caused
by physical mechanisms as a gas
temperature drift the major
reason of the first
wafer effect
in semiconductor manufacturing. The second parameter,
the spatially avaraged electron density shows usually a close
relation to the pure physical mechanisms as sputter etching.
|
| Literature: |
Please visit our
download area, in particular the section
of Fundamental Papers or contact
us via mail in case of further interest.
|